A brief introduction to “anelastic spectroscopy”
Anelastic spectroscopy consists in perturbing the energy levels of mobile species (atoms, point-defect complexes, structure units, dislocations, polarons, etc.) by applying an external stress to the sample, and by measuring their diffusion parameters while they, by thermal activation, are attempting to reach the new equilibrium by redistribution among the perturbed levels.
The externally applied stress interacts with the lattice distortion introduced by the defects and makes some defect orientations energetically preferred with respect to others.
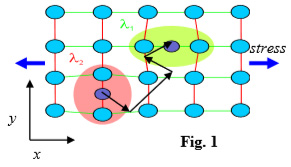
In the example of Fig. 1 an applied x-stress dilates the sites of the defects in orientation x and contracts the y-defects. The consequent deepening of the site-energy of x-defects makes them energetically favoured. As a consequence, a thermally-assisted and diffusion-controlled enrichment of x-sites and a correspondent depletion of y-sites takes place.
The lattice distortion associated with the defect is represented by the so-called elastic dipole l, which is a second rank tensor, and in the present example it has two independent orientations, l1 and l2. The quantity t is the relaxation time of the defect-reorientation process, and l reorients itself concomitantly. The relaxation time is very close to the jumping time of the species, and follows different laws according to the nature of the particular process.
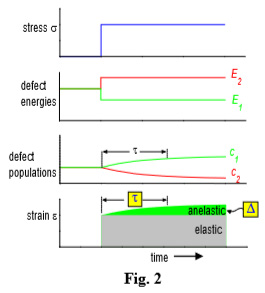
Classically t follows the Arrhenius law , where E is the activation enthalpy. The alignment of the microscopic distortions along x results in a time-delayed macroscopic strain, called anelastic strain, which is summed up to the instantaneous elastic strain, as depicted in Fig. 2. The relative height of the anelastic strain is called relaxation strength, D=ean/eel ~ (Dl)2/T, where Dl is the variation of the elastic dipole when defects reorient themselves.
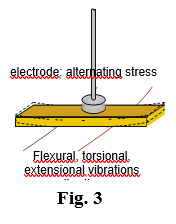
Dynamic experiments. The external stress is most sensitively applied through the vibration, by electrostatically exciting the various vibration modes of rectangular bars.
Figure 3 shows the suspension of a vibrating sample on its nodal lines by thin wires, in order to reduce the background dissipation to a minimum, and Fig. 4 a detail of the experimental cell. The sample may be bulky, or a powder consolidated by compression or sintering. This measurement is extremely sensitive; indeed, the vibration amplitudes may by as low as 1-10 nm, introducing site-energy shifts of ~ 10-7 eV. An anelastic relaxation experiment supplies the measurement of the complex elastic modulus: M(ω)= M’(ω)+ jM”(ω)
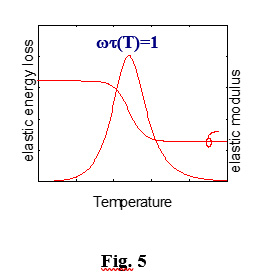
and has a maximum for wt=1 (w, angular vibration frequency), as shown in Fig. 5. In concomitance with the evolution of the dissipation peak, the modulus undergoes a jump produced by the relaxation, called modulus defect.
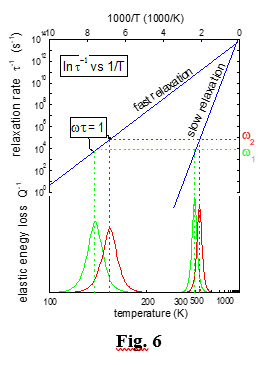
The dissipation Q-1 is measured from the decay of the vibration amplitude or from the width of the resonance curve, whereas the elastic modulus is measured by the sample vibration frequency, as M’(ω) ~ f 2. During vibration, the sites of the mobile species which were made energetically favoured in the first half period become unfavoured in the second half. By varying temperature, and hence t(T), when the relaxation condition is reached (ω =1/t), the angular vibration frequency is equal to the relaxation rate, and dissipation reaches its maximum as the stimulated atomic migration is able to follow the applied vibration. At the higher vibration modes the Debye peak is shifted to higher temperature, because the relaxation condition is reached at higher T, as depicted in Fig. 6. The analysis of the peak shift is generally used to know whether a process is due to a thermally activated motion, and to measure the activation energy and the other motion parameters.

Slow processes are found at high temperature, and fast processes at low T (Fig. 6). Thus, a temperature scan can reveal the dynamics of the various mobile species, whose peaks appear selectively in different positions on the temperature scale according to their mobility.
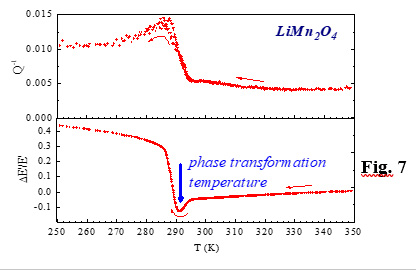
A phase transformation is revealed by an inflection or a jump of the frequency curve, which is often accompanied by a dissipation spike, as schematically shown in Fig. 7. However, in this case the temperatures at which these features occur are not dependent on frequency but on the transformation temperatures themselves.
In summary, anelastic spectroscopy gives essential information often not obtainable by other techniques. It is complementary to neutron scattering, NMR, NQR. It supplies two simultaneous and independent measurements as a function of temperature and frequency:
- i) the coefficient of elastic energy dissipation, Q-1, which gives the dynamics of mobile species including jumping time, diffusion parameters, activation energy, interaction, classical or quantum regime;
- ii) the elastic modulus, M’(w), which is very sensitive to the phase transformations and the formation of different symmetry particles and precipitations, and for monitoring “in situ” the time evolution of the chemical reactions.